Assalamualaikum wr. wb
Selamat datang kembali di blog kami, kali ini kita akan membahas tentang Persamaan Differensial Faktor Integral.
Persamaan Diferensial Non Eksak adalah suatu Persamaan Dasar tingkat satu danberpangkat satu yang berbentuk:
Selamat datang kembali di blog kami, kali ini kita akan membahas tentang Persamaan Differensial Faktor Integral.
Persamaan Diferensial Non Eksak adalah suatu Persamaan Dasar tingkat satu danberpangkat satu yang berbentuk:
M(x,y) dx + N(x,y) dy = 0 (1)
dan memenuhi syarat:
Penyelesaian Persamaan Diferensial Non Eksak dapat diperoleh dengan mengalikan pers. 1 dengan suatu fungsi u yang disebut Faktor Integral (FI) sehingga diperoleh PD Eksak yaitu:
u M(x,y) dx + u N(x,y) dy = 0 (2)
karena PD (pers. 2) sudah berbentuk eksak, maka memenuhi :
Rumus Umum FI :
secara umum FI u terdiri dari tiga kondisi yaitu:
1. FI u sebagai fungsi x saja
2. FI u sebagai fungsi y saja
3. FI u sebagai fungsi x dan y
karena u sebagai fungsi x saja, maka:
sehingga pers. 3 dapat ditulis menjadi:
karena u sebagai fungsi y saja, maka:
sehingga pers. 3 dapat ditulis:
FI : u = u (x,y)
Jika bentuk peubah x,y = v, maka FI : u = u (v)
Jikapers. 4,5 dan 6 disubtitusikan ke pers. 3, maka:
Terimakasih, semoga bermanfaat






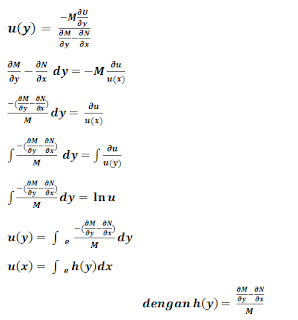


Comments
Post a Comment